堆
堆的基本操作
堆是具有以下性质的完全二叉树,有两种堆:
- 大顶堆(大根堆):每个节点值大于等于左、右孩子节点的值,大根堆的堆顶是整个堆中的最大元素。
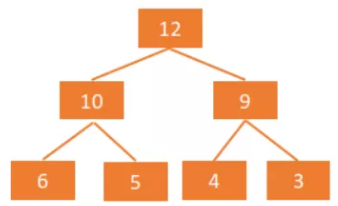
- 小顶堆(小根堆):每个节点值小于等于左、右孩子节点的值,小根堆的堆顶是整个堆中的最小元素。
存储形式:数组。
应用:优先级队列(多个定时器任务问题)、求前n个最大/最小的数。
堆的基本操作包括(均依赖于堆的自我调整使其满足大/小根堆特性):
- 插入节点:插入位置是在堆的末尾,然后对该节点进行上浮操作(上浮即和它的父节点比较大小);
- 删除节点:删除位置在堆顶,然后将堆尾元素放到堆顶,对此元素进行下沉操作(下沉即和它的左、右孩子比较大小),不断递归,直到无法下沉;
- 构建堆:把一个无序的完全二叉树调整为大/小根堆,从下往上、从左往右的对所有非叶子节点进行下沉操作。
设计堆
利用数组,实现具有插入,删除操作的大根或小根堆。
class Heap {
container: number[];
cmp: Function;
/**
* 默认是大顶堆
* @param type
*/
constructor(type: 'max' | 'min' = 'max') {
this.container = [];
this.cmp = type === 'max' ? (x: number, y: number) => x > y : (x: number, y: number) => x < y;
}
/**
* 对堆中的两个节点进行交换
* @param i
* @param j
*/
swap(i: number, j: number) {
[this.container[i], this.container[j]] = [this.container[j], this.container[i]];
}
/**
* 插入节点,在堆末尾插入,并对节点进行上浮操作
* @param data
* @returns
*/
insert(data: number) {
this.container.push(data);
// 上浮操作
let index = this.container.length - 1;
while (index) {
// 直到遍历到堆顶
// 父节点位置
const parent = Math.floor((index - 1) / 2);
if (!this.cmp(this.container[index], this.container[parent])) {
// 大顶堆:当前节点不大于父节点,到达最终位置
return;
}
// 交换
this.swap(index, parent);
index = parent;
}
}
/**
* 删除节点,删除堆顶元素与堆尾元素后的堆尾所在元素,再对堆顶元素执行下沉操作
* @returns
*/
delete(): number {
if (this.isEmpty()) return NaN;
// 将堆顶元素与堆尾元素进行交换,并删除堆尾元素
const size = this.getSize();
this.swap(0, size - 1);
const top = this.container.pop()!;
// 当前节点位置
let index = 0;
// 交换节点位置,大顶堆:子节点中的较大者
let exchange = index * 2 + 1;
while (exchange < size) {
// 右子节点位置
const right = index * 2 + 2;
if (right < this.container.length && this.cmp(this.container[right], this.container[exchange])) {
// 大顶堆:存在右节点且右节点较大
exchange = right;
}
if (!this.cmp(this.container[exchange], this.container[index])) {
// 大顶堆:子节点较大者小于当前节点
return NaN;
}
// 交换
this.swap(exchange, index);
index = exchange;
exchange = index * 2 + 1;
}
return top;
}
/**
* 获取堆顶元素,堆空则返回 NaN
* @returns
*/
top(): number {
if (this.isEmpty()) return NaN;
return this.container[0];
}
/**
* 判断堆是否为空
* @returns
*/
isEmpty(): boolean {
return this.getSize() === 0;
}
/**
* 堆中元素个数
* @returns
*/
getSize(): number {
return this.container.length;
}
}算法题
1. 数据流中的中位数
题目描述:如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。例如, [2,3,4] 的中位数是 3, [2,3] 的中位数是 (2 + 3) / 2 = 2.5
分析:
冒泡/二分插入有序法,首先对于每个插入的元素,在插入时使其有序,取出时只需要取中间的数或中间两个数和的一半即可。
大小根堆划分法,使用大根堆和小根堆分别保存较小和较大的一半,且在插入时保证,且小根堆比大根堆中元素个数多1或相等,如此一来,在取出时若两个堆元素个数相等,则中位数是两个堆顶元素的一半,否则是中位数是小根堆的堆顶。
求解:
class Heap {
container: number[];
cmp: Function;
/**
* 默认是大顶堆
* @param type
*/
constructor(type: 'max' | 'min' = 'max') {
this.container = [];
this.cmp = type === 'max' ? (x: number, y: number) => x > y : (x: number, y: number) => x < y;
}
/**
* 对堆中的两个节点进行交换
* @param i
* @param j
*/
swap(i: number, j: number) {
[this.container[i], this.container[j]] = [this.container[j], this.container[i]];
}
/**
* 插入节点,在堆末尾插入,并对节点进行上浮操作
* @param data
* @returns
*/
insert(data: number) {
this.container.push(data);
// 上浮操作
let index = this.container.length - 1;
while (index) {
// 直到遍历到堆顶
// 父节点位置
const parent = Math.floor((index - 1) / 2);
if (!this.cmp(this.container[index], this.container[parent])) {
// 大顶堆:当前节点不大于父节点,到达最终位置
return;
}
// 交换
this.swap(index, parent);
index = parent;
}
}
/**
* 删除节点,删除堆顶元素与堆尾元素后的堆尾所在元素,再对堆顶元素执行下沉操作
* @returns
*/
delete(): number {
if (this.isEmpty()) return NaN;
// 将堆顶元素与堆尾元素进行交换,并删除堆尾元素
const size = this.getSize();
this.swap(0, size - 1);
const top = this.container.pop()!;
// 当前节点位置
let index = 0;
// 交换节点位置,大顶堆:子节点中的较大者
let exchange = index * 2 + 1;
while (exchange < size) {
// 右子节点位置
const right = index * 2 + 2;
if (right < this.container.length && this.cmp(this.container[right], this.container[exchange])) {
// 大顶堆:存在右节点且右节点较大
exchange = right;
}
if (!this.cmp(this.container[exchange], this.container[index])) {
// 大顶堆:子节点较大者小于当前节点
return NaN;
}
// 交换
this.swap(exchange, index);
index = exchange;
exchange = index * 2 + 1;
}
return top;
}
/**
* 获取堆顶元素,堆空则返回 NaN
* @returns
*/
top(): number {
if (this.isEmpty()) return NaN;
return this.container[0];
}
/**
* 判断堆是否为空
* @returns
*/
isEmpty(): boolean {
return this.getSize() === 0;
}
/**
* 堆中元素个数
* @returns
*/
getSize(): number {
return this.container.length;
}
}import Heap from '../堆的设计与实现/heap';
// 二分查找插入法
class MedianFinder {
data: number[];
// 或者使用一个大根堆和一个小根堆分别保存一半的元素
minPart: Heap; // 较小的一半使用大根堆保存
maxPart: Heap; // 较大的一半使用小根堆保存
constructor() {
this.data = [];
this.minPart = new Heap('max');
this.maxPart = new Heap('min');
}
/**
* 从数据流中添加一个整数到数据结构中: 大小根堆法
* @param num
*/
addNumHeap(num: number): void {
if (this.minPart.isEmpty() || num <= this.minPart.top()) {
// 小于较小的一半
this.minPart.insert(num);
if (this.maxPart.getSize() + 1 < this.minPart.getSize()) {
// 较小的一半中元素个数比较大的一半中元素少2个
this.maxPart.insert(this.minPart.delete());
}
} else {
this.maxPart.insert(num);
if (this.maxPart.getSize() > this.minPart.getSize()) {
// 较小的一半中元素个数比较大的一半中元素多1个
this.minPart.insert(this.maxPart.delete());
}
}
}
/**
* 从数据流中添加一个整数到数据结构中: 二分法
* @param num
*/
addNumBinary(num: number): void {
const size = this.data.length;
if (size === 0) {
// 数据结构为空
this.data.push(num);
return;
}
let left = 0;
let right = size - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2); // (left + right) >> 1;
const midNum = this.data[mid];
if (midNum === num) {
// 在该位置插入
this.data.splice(mid, 0, num);
return;
}
if (midNum > num) {
// 插入位置在 [left, mid - 1];
right = mid - 1;
} else {
// 插入位置在 [mid + 1, right];
left = mid + 1;
}
}
this.data.splice(left, 0, num);
}
/**
* 从数据流中添加一个整数到数据结构中: 冒泡法
* @param num
* @returns
*/
addNumBubble(num: number): void {
this.data.push(num);
const size = this.data.length;
for (let i = size - 2; i >= 0 && this.data[i] > this.data[i + 1]; i -= 1) {
// 交换
[this.data[i], this.data[i + 1]] = [this.data[i + 1], this.data[i]];
}
}
/**
* 返回目前所有元素的中位数: 二分法。
*/
findMedianBinary(): number {
const size = this.data.length;
const mid = Math.floor(size / 2);
if (size & 1) {
// 奇数
return (this.data[mid - 1] + this.data[mid]) / 2;
}
return this.data[mid];
}
/**
* 返回目前所有元素的中位数。大小根堆法
*/
findMedianHeap(): number {
if (this.minPart.getSize() > this.maxPart.getSize()) {
return this.minPart.top();
}
return (this.minPart.top() + this.maxPart.top()) / 2.0;
}
}Hash 表
Hash 表的基本操作
Hash 表是一种是使用哈希函数来组织数据,支持快速插入和搜索的线性数据结构。关键是通过哈希函数将键映射到存储桶。哈希函数的选取取决于键的值范围和桶的数量。
- 插入新的键,哈希函数计算被存储的桶;
- 搜索一个键,使用相同的哈希函数计算所在桶, 然后在桶中搜索。
设计 Hash 表
关键是选择哈希函数和进行冲突处理。
哈希函数:分配一个地址存储值。理想情况下,每个键都应该有一个对应唯一的散列值。
冲突处理:哈希函数的本质就是从 A 映射到 B。但是多个 A 键可能映射到相同的 B。
冲突解决策略:
- 单独链接法(链表法):对于相同的散列值,我们将它们放到一个桶中,每个桶是相互独立的。
import MyLinkedList from '../../链表/设计链表/linkList';
import defaultToString from './defaultToString';
// 单独链接法(链表)
export default class HashTableSeparateChaining<K, V> {
protected table: Map<number, MyLinkedList<{ key: K; value: V }>>;
constructor(protected toStrFn: (key: K) => string = defaultToString) {
this.table = new Map();
}
/**
* @description: 哈希函数(djb2函数(或者loselose函数)
*/
private hashCodeHelper(key: K): number {
if (typeof key === 'number') {
return key;
}
const tableKey = this.toStrFn(key);
let hash = 5381;
for (let i = 0; i < tableKey.length; i += 1) {
hash = hash * 33 + tableKey.charCodeAt(i);
}
return hash % 1013;
}
/**
* @description: 哈希函数封装
*/
hashCode(key: K): number {
return this.hashCodeHelper(key);
}
/**
* @description: 更新散列表
*/
put(key: K, value: V): boolean {
if (key !== null && value !== null) {
const position = this.hashCode(key);
// 当该 hashcode 不存在时,先创建一个链表
if (this.table.get(position) == null) {
this.table.set(position, new MyLinkedList<{ key: K; value: V }>());
}
// 再给链表push值
this.table.get(position)!.addAtTail({ key, value });
return true;
}
return false;
}
/**
* @description: 根据键获取值
*/
get(key: K): V | undefined {
const position = this.hashCode(key);
const linkedList = this.table.get(position);
if (linkedList && linkedList.size !== 0) {
let current = linkedList.head;
// 去链表中迭代查找键值对
while (current !== null) {
if (current.val.key === key) {
return current.val.value;
}
current = current.next;
}
}
}
/**
* @description: 根据键移除值
*/
remove(key: K): boolean {
const position = this.hashCode(key);
const linkedList = this.table.get(position);
if (linkedList && linkedList.size !== 0) {
let current = linkedList.head;
let index = 0;
while (current !== null) {
if (current.val.key === key) {
break;
}
index += 1;
current = current.next;
}
linkedList.deleteAtIndex(index);
// 关键的一点,当链表为空以后,需要在 table 中删除掉 hashcode
if (linkedList.size === 0) {
this.table.delete(position);
}
return true;
}
return false;
}
/**
* @description: 返回是否为空散列表
*/
isEmpty(): boolean {
return this.size() === 0;
}
/**
* @description: 散列表的大小
*/
size(): number {
let count = 0;
// 迭代每个链表,累计求和
for (const [hashCode, linkedList] of this.table) {
count += linkedList.size;
}
return count;
}
/**
* @description: 清空散列表
*/
clear() {
this.table.clear();
}
/**
* @description: 返回内部table
*/
getTable() {
return this.table;
}
/**
* @description: 替代默认的toString
*/
toString(): string {
if (this.isEmpty()) {
return '';
}
const objStringList: string[] = [];
for (const [hashCode, linkedList] of this.table) {
let node = linkedList.head;
while (node) {
objStringList.push(`{${node.val.key} => ${node.val.value}}`);
node = node.next;
}
}
return objStringList.join(',');
}
}/**
* @description: 将 item 也就是 key 统一转换为字符串
*/
export default function defaultToString(item: any): string {
// 对于 null undefined和字符串的处理
if (item === null) {
return 'NULL';
}
if (item === undefined) {
return 'UNDEFINED';
}
if (typeof item === 'string' || item instanceof String) {
return `${item}`;
}
// 其他情况时调用数据结构自带的 toString 方法
return item.toString();
}- 开放地址法(线性探测):每当有碰撞,则根据我们探查的策略找到一个空的槽为止。
import defaultToString from './defaultToString';
// 开放地址法(线性探测)
export default class HashTableLinearProbing<K, V> {
protected table: Map<number, { key: K; value: V }>;
constructor(protected toStrFn: (key: K) => string = defaultToString) {
this.table = new Map();
}
/**
* @description: 哈希函数(djb2函数(或者loselose函数)
*/
private hashCodeHelper(key: K): number {
if (typeof key === 'number') {
return key;
}
const tableKey = this.toStrFn(key);
let hash = 5381;
for (let i = 0; i < tableKey.length; i += 1) {
hash = hash * 33 + tableKey.charCodeAt(i);
}
return hash % 1013;
}
/**
* @description: 哈希函数封装
*/
hashCode(key: K): number {
return this.hashCodeHelper(key);
}
/**
* @description: 更新散列表
*/
put(key: K, value: V): boolean {
if (key !== null && value !== null) {
const position = this.hashCode(key);
if (this.table.get(position) == null) {
// 当hashcode位置为空时,可以直接添加
this.table.set(position, { key, value });
} else {
// 否则需要迭代查找最近的空位置再添加
let index = position + 1;
while (this.table.get(index) !== null) {
index += 1;
}
this.table.set(index, { key, value });
}
return true;
}
return false;
}
/**
* @description: 根据键获取值
*/
get(key: K): V | undefined {
const position = this.hashCode(key);
if (this.table.get(position)) {
// 如果查到的hashcode位置就是要查的key,则直接返回
if (this.table.get(position)!.key === key) {
return this.table.get(position)!.value;
}
// 否则需要迭代着向下查找
let index = position + 1;
while (this.table.get(index) != null && this.table.get(index)!.key !== key) {
index += 1;
}
if (this.table.get(index) !== null && this.table.get(index)!.key === key) {
return this.table.get(position)!.value;
}
}
// 最后也没查到,就返回 undefined
return undefined;
}
/**
* @description: 根据键移除值
*/
remove(key: K): boolean {
const position = this.hashCode(key);
if (this.table.get(position)) {
// 同理,如果hashcode对应位置就是要查的key,则直接删除
if (this.table.get(position)!.key === key) {
this.table.delete(position);
// 删除后处理副作用
this.verifyRemoveSideEffect(key, position);
return true;
}
// 同理,如果hashcode对应的位置不是要查的key,就迭代查到
let index = position + 1;
while (this.table.get(index) !== null && this.table.get(index)!.key !== key) {
index += 1;
}
if (this.table.get(index) !== null && this.table.get(index)!.key === key) {
this.table.delete(index);
// 同样在删除后处理副作用
this.verifyRemoveSideEffect(key, index);
return true;
}
}
return false;
}
/**
* @description: 处理移除键值对后的副作用
*/
private verifyRemoveSideEffect(key: K, removedPosition: number) {
const hash = this.hashCode(key);
let index = removedPosition + 1;
// 迭代着处理后面的每一个键值对
while (this.table.get(index) !== null) {
const posHash = this.hashCode(this.table.get(index)!.key);
// 挨个向前挪动,关键点在于,hashcode值比较小的键值对尽量先向前补位
// 详细的说:如果当前元素的 hash 值小于或等于原始的 hash 值
// 或者当前元素的 hash 值小于或等于 removedPosition(也就是上一个被移除 key 的 hash 值),
// 表示我们需要将当前元素移动至 removedPosition 的位置
if (posHash <= hash || posHash <= removedPosition) {
this.table.set(removedPosition, this.table.get(index)!);
this.table.delete(index);
removedPosition = index;
}
index += 1;
}
}
/**
* @description: 返回是否为空散列表
*/
isEmpty(): boolean {
return this.size() === 0;
}
/**
* @description: 散列表的大小
*/
size(): number {
return this.table.size;
}
/**
* @description: 清空散列表
*/
clear() {
this.table.clear();
}
/**
* @description: 返回内部table
*/
getTable(): Map<number, { key: K; value: V }> {
return this.table;
}
/**
* @description: 替代默认的toString
*/
toString(): string {
if (this.isEmpty()) {
return '';
}
const objStringList: string[] = [];
for (const [hashCode, { key, value }] of this.table) {
objStringList.push(`{${key} => ${value}}`);
}
return objStringList.join(',');
}
}/**
* @description: 将 item 也就是 key 统一转换为字符串
*/
export default function defaultToString(item: any): string {
// 对于 null undefined和字符串的处理
if (item === null) {
return 'NULL';
}
if (item === undefined) {
return 'UNDEFINED';
}
if (typeof item === 'string' || item instanceof String) {
return `${item}`;
}
// 其他情况时调用数据结构自带的 toString 方法
return item.toString();
}上述实现中使用到的 djb2 函数(或者 loselose 函数),原理是借助字符串各个位上的 UTF-16 Unicode 值进行计算,然后对特定值取余即为哈希值。
- 双散列法:使用两个哈希函数计算散列值,选择碰撞更少的地址。
JavaScript 内置哈希表的典型设计是: 键值可以是任何具有可哈希码(映射函数获取存储区索引)的可哈希化的类型。每个桶包含一个数组,用于在初始时将所有值存储在同一个桶中。 如果在同一个桶中有太多的值,这些值将被保留在一个**高度平衡的二叉树搜索树(BST)**中。 插入和搜索的平均时间复杂度仍为 O(1)。最坏情况下插入和搜索的时间复杂度是 O(logN)。使用高度平衡的 BST 是在插入和搜索之间的一种权衡。
 Silver Bullet
Silver Bullet