栈

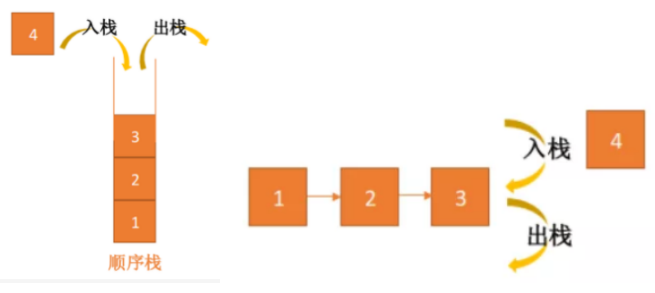
栈是一种后入先出（LIFO）的线性逻辑存储结构。只允许在栈顶进行进出操作。

栈基本操作

基本操作包括：入栈（push）/出栈（pop）/获取栈顶元素（peek）。

栈的实现主要有两种：

数组实现，即顺序栈；
链表实现，即链式栈。

无论是以数组还是以链表实现，入栈、出栈的时间复杂度都是O(1)。

栈的应用比如函数执行/括号匹配/表达式计算/浏览器前进后退。

设计栈

1. 数组实现栈

// 数组栈
export default class ArrayStack<T> {
  items: T[];

  constructor() {
    this.items = [];
  }

  /**
   * 入栈
   * @param item
   */
  push(item: T) {
    this.items.push(item);
  }

  /**
   * 出栈
   * @returns
   */
  pop() {
    if (this.isEmpty) throw new Error('栈空');
    return this.items.pop();
  }

  /**
   * 获取栈顶元素
   * @returns
   */
  peek() {
    if (this.isEmpty) throw new Error('栈空');
    return this.items[this.size - 1];
  }

  /**
   * 判空
   * @returns
   */
  get isEmpty() {
    return this.size === 0;
  }

  /**
   * 获取栈元素的个数
   * @returns
   */
  get size() {
    return this.items.length;
  }
}

2. 链表实现栈

linkStack.tslinkNode.ts

import LinkNode from '../../链表/设计链表/linkNode';

// 链表栈
export default class LinkStack<T> {
  // 栈的长度
  size: number;

  // 栈顶指针
  top: LinkNode<T> | null;

  constructor() {
    this.size = 0;
    this.top = null;
  }

  /**
   * 入栈
   * @param item
   */
  push(val: T) {
    const node = new LinkNode(val);
    if (this.isEmpty) {
      // 栈空
      this.top = node;
    } else {
      // 栈非空
      node.next = this.top;
      this.top = node;
    }
    this.size += 1;
  }

  /**
   * 出栈
   * @returns
   */
  pop() {
    if (this.isEmpty) {
      // 栈空
      throw new Error('栈空');
    }
    // 栈非空
    const data = this.top!.val; // 栈顶元素值
    this.top = this.top!.next; // 新栈顶
    this.size -= 1;
    return data;
  }

  /**
   * 获取栈顶元素
   * @returns
   */
  peek() {
    if (this.isEmpty) {
      // 栈空
      throw new Error('栈空');
    }
    return this.top!.val;
  }

  /**
   * 判空
   * @returns
   */
  get isEmpty() {
    return this.top === null;
  }
}

// 节点
export default class LinkNode<T> {
  val: T;

  next: LinkNode<T> | null;

  constructor(val: T, next?: LinkNode<T> | null) {
    this.val = val;
    this.next = next ?? null;
  }
}

算法题

1. 包含 min 函数的栈

题目描述：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

分析：

数据栈+最小栈法，利用一个最小栈存放当前数据栈的最小元素，保持两个栈的长度相同。从首个元素入数据栈开始，每个元素均入数据栈。同时，判断当前元素与最小栈栈顶元素的大小，将小的元素入最小栈即可。

求解：

// 数据栈+最小栈法
class MinStack {
  dataStack: number[];

  minStack: number[];

  constructor() {
    this.dataStack = [];
    this.minStack = [];
  }

  push(x: number): void {
    const dataSize = this.dataStack.length;
    const minSize = this.minStack.length;
    if (dataSize === 0 || this.minStack[minSize - 1] > x) {
      this.minStack.push(x);
    } else {
      this.minStack.push(this.minStack[minSize - 1]);
    }
    this.dataStack.push(x);
  }

  pop(): void {
    const dataSize = this.dataStack.length;
    if (dataSize) {
      this.minStack.pop();
      this.dataStack.pop();
    }
  }

  top(): number {
    const dataSize = this.dataStack.length;
    if (dataSize) {
      return this.dataStack[dataSize - 1];
    }
    return NaN;
  }

  min(): number {
    const minSize = this.dataStack.length;
    if (minSize) {
      return this.minStack[minSize - 1];
    }
    return NaN;
  }
}

2. 栈的压入、弹出序列

题目描述：输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

分析：

辅助栈模拟法，借用一个辅助栈 stack ，模拟压入/弹出操作的排列。根据是否模拟成功，即可得到结果。首先按照压栈序列的顺序执行辅助栈入栈操作，每次压栈序列中的元素入栈时，若栈不为空且栈顶元素等于弹出序列当前应弹出元素，即对栈进行出栈操作并更新弹出元素，最终判断栈是否为空即可。

求解：

// 辅助栈模拟法
export default function validateStackSequences(pushed: number[], popped: number[]): boolean {
  const stack: number[] = [];
  const size = pushed.length;
  // 弹出序列当前应该弹出元素的下标
  let poppedIndex = 0;
  // 出栈和入栈序列不全为空
  for (let i = 0; i < size; i += 1) {
    const element = pushed[i];
    // 将入栈序列元素入栈
    stack.push(element);
    while (stack.length && stack[stack.length - 1] === popped[poppedIndex]) {
      // 栈不为空 且 栈顶元素等于弹出序列当前应弹出元素
      stack.pop();
      // 下一个应该弹出元素的下标
      poppedIndex += 1;
    }
  }
  return stack.length === 0; // 弹出与压入对应说明满足
}

队列

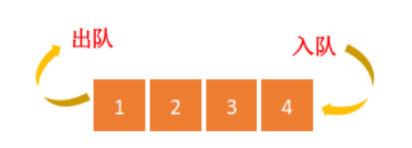
队列是一种先入先出（FIFO）的线性逻辑存储结构。只允许在队首进行出队（即 delete 删除）操作，队尾进行入队（即 insert 插入）操作。

队列基本操作

队列的基本操作包括：入队（enqueue）/ 出队（dequeue）/ 获取队头元素（peek）

队列的实现主要有两种：

数组实现，即顺序队列。
链表实现，即链式队列。

无论是以数组还是以链表实现，入队、出队的时间复杂度都是 O(1)。

队列的应用比如线程池、资源池、消息队列、异步队列。

设计队列

1.顺序队列

数组实现，使用shift出队时每次都要移动队列元素，效率不高。改进方案是可以队列初始化时就需要规定队列长度，通过判断队尾是否有空间，有就让元素一直入队，直到队尾没有空间位置，然后进行整体进行一次搬移，这样优化了入队的效率，平均时间复杂度还是 O(1)。

// 数组实现顺序队列
export default class ArrayQueue<T> {
  items: T[];

  constructor() {
    this.items = [];
  }

  /**
   * 入队
   * @param item
   */
  push(item: T) {
    this.items.push(item);
  }

  /**
   * 出队
   * @returns
   */
  pop() {
    if (this.isEmpty()) throw new Error('队列空');
    return this.items.shift();
  }

  /**
   * 获取队顶元素
   * @returns
   */
  peek() {
    if (this.isEmpty()) throw new Error('队列空');
    return this.items[0];
  }

  /**
   * 判空
   * @returns
   */
  isEmpty() {
    return this.items.length === 0;
  }

  /**
   * 获取队元素的个数
   * @returns
   */
  getSize() {
    return this.items.length;
  }
}

2.循环队列

数组实现，初始化需指定队列容量，留一个空位，队空条件 head = tail，队满条件 head =( tail + 1) % capacity，队列元素个数 (tail - head + capacity) % capacity。

// 数组循环队列
export default class LoopQueue {
  // 存放元素的数组
  values: (number | undefined)[];

  // 当前元素个数
  count: number;

  // 队的长度
  capacity: number;

  // 队尾
  head: number;

  // 队尾
  tail: number;

  constructor(capacity: number) {
    this.head = 0;
    this.tail = 0;
    this.capacity = capacity;
    this.count = 0;
    this.values = new Array(capacity);
  }

  /**
   * 入队
   * @param item
   */
  enQueue(val: number) {
    if (this.isFull()) {
      throw new Error('队满');
    }
    this.values[this.tail] = val;
    this.tail = (this.tail + 1) % this.capacity;
    this.count += 1;
    return true;
  }

  /**
   * 出队
   * @returns
   */
  deQueue(): number {
    if (this.isEmpty()) {
      throw new Error('队空');
    }
    const value = this.values[this.head] as number;
    this.values[this.head] = undefined;
    this.head = (this.head + 1) % this.capacity;
    this.count -= 1;
    return value;
  }

  /**
   * 获取队头元素
   * @returns
   */
  peek() {
    if (this.isEmpty()) {
      throw new Error('队空');
    }
    const value = this.values[this.head];
    return value;
  }

  /**
   * 判空
   * @returns
   */
  isEmpty() {
    // 或 return this.head === this.tail
    return this.count === 0;
  }

  /**
   * 判满
   * @returns
   */
  isFull() {
    // 或 return this.head === (this.tail + 1) % this.capacity
    return this.count === this.capacity - 1;
  }

  /**
   * 获取队元素的个数
   * @returns
   */
  getSize() {
    return this.count;
  }

  /**
   * 清空队列
   * @returns
   */
  clear() {
    this.head = 0;
    this.tail = 0;
    this.count = 0;
    this.values = new Array(this.capacity);
    return true;
  }
}

3.链式队列

链表实现，链表尾入队，链表头出队。

linkQueue.tslinkNode.ts

import LinkNode from '../../链表/设计链表/linkNode';

// 链表顺序队列
export default class LinkQueue<T> {
  // 队的长度
  size: number;

  // 队尾指针
  head: LinkNode<T> | null;

  // 队尾指针
  tail: LinkNode<T> | null;

  constructor() {
    this.size = 0;
    this.head = null;
    this.tail = null;
  }

  /**
   * 入队
   * @param item
   */
  enQueue(val: T) {
    const node = new LinkNode(val);
    if (this.size === 0) {
      this.head = node;
      this.tail = node;
    } else {
      this.tail!.next = node;
      this.tail = this.tail!.next;
    }
    this.size += 1;
  }

  /**
   * 出队
   * @returns
   */
  deQueue() {
    if (this.size === 0) {
      // 队空
      throw new Error('队空');
    } else {
      // 队非空
      const node = this.head;
      this.head = node!.next;
      this.size -= 1;
      return node!.val;
    }
  }

  /**
   * 获取队头元素
   * @returns
   */
  peek() {
    if (this.size === 0) {
      // 队空
      throw new Error('队空');
    } else {
      return this.head!.val;
    }
  }

  /**
   * 判空
   * @returns
   */
  isEmpty() {
    return this.size === 0;
  }

  /**
   * 获取队元素的个数
   * @returns
   */
  getSize() {
    return this.size;
  }
}

// 节点
export default class LinkNode<T> {
  val: T;

  next: LinkNode<T> | null;

  constructor(val: T, next?: LinkNode<T> | null) {
    this.val = val;
    this.next = next ?? null;
  }
}

算法题

1. 两个栈实现队列

题目描述：用两个栈来实现一个队列，完成队列的Push和Pop操作。队列中的元素为int类型。

分析：

栈用数组模拟，队列只允许在队首进行出队（即delete/pop删除）操作，队尾进行入队（即insert/push插入）操作，因此其中一个栈 stack1用于入队，另一个栈stack2用于出队，出队时判断出队栈 stack2 是否为空：

空则将入队栈 stack1 中的元素全部转移至出队栈 stack2，然后出队栈 stack2 栈顶元素出队即可。
非空，则出队栈 stack2 栈顶元素直接出队。

求解：

// 数组模拟
class CQueue {
  pushStack: number[];

  popStack: number[];

  constructor() {
    this.pushStack = [];
    this.popStack = [];
  }

  appendTail(value: number): void {
    this.pushStack.push(value);
  }

  deleteHead(): number {
    if (this.pushStack.length === 0 && this.popStack.length === 0) {
      // 队列为空
      return -1;
    }
    // 出队的栈为空时，依次将入队的栈中元素先入出队的栈
    if (this.popStack.length === 0) {
      while (this.pushStack.length) {
        this.popStack.push(this.pushStack.pop()!);
      }
    }
    return this.popStack.pop()!;
  }
}

数据结构与算法

网络

css

javascript

栈

栈基本操作

设计栈

1. 数组实现栈

2. 链表实现栈

算法题

1. 包含 min 函数的栈

2. 栈的压入、弹出序列

队列

队列基本操作

设计队列

1.顺序队列

2.循环队列

3.链式队列

算法题

1. 两个栈实现队列

栈 ​

栈基本操作 ​

设计栈 ​

1. 数组实现栈 ​

2. 链表实现栈 ​

算法题 ​

1. 包含 min 函数的栈 ​

2. 栈的压入、弹出序列 ​

队列 ​

队列基本操作 ​

设计队列 ​

1.顺序队列 ​

2.循环队列 ​

3.链式队列 ​

算法题 ​

1. 两个栈实现队列 ​

栈

栈基本操作

设计栈

1. 数组实现栈

2. 链表实现栈

算法题

1. 包含 min 函数的栈

2. 栈的压入、弹出序列

队列

队列基本操作

设计队列

1.顺序队列

2.循环队列

3.链式队列

算法题

1. 两个栈实现队列